How fast is a river? A common question without a simple answer. Flow speed and rate vary depending on the characteristics of the channel that the fluid flows through. Specifically, the channel’s slope, size and surface roughness affect a river’s flow. The relationship between flow and these channel characteristics is represented in the Manning equation, which can be adjusted to determine both velocity and flowrate:
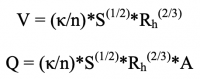
Where:
V = velocity
Q = flowrate
κ = conversion factor = 1.00 (metric), 1.49 (British)
n = channel roughness = 0.035 (value applies only to major rivers) S = channel slope = ~.004
Rh = hydraulic radius = Area/Wetted Perimeter
A = area
Velocity measurements were taken with the Grande Ronde above La Grande (river mile 172.8) and at the confluence with the Wallowa River (river mile 81.5). The results of both the measured and calculated flowrate are shown in table 1:

The large percent difference can be largely attributed to the assumption that the measured cross-sections were uniformly shaped as a rectangle rather than as a parabola. The additional area of the rectangular cross-section would account for the additional flow that the Manning equation predicts This would be a major source or error as those values are counted twice in the calculation: first in the hydraulic radius and again in the area. Also, another source of error is the assumption that the slope of the Grande Ronde is uniform for the entire length of the river. While this assumption is less likely to have produced such a large error, it would still affect the final results.

Figure 1: Discharge measurement location along the Grande Ronde River immediately above the confluence with the Wallowa River (RM 81.5)

Figure 2: Discharge measurement location along the Upper Grande Ronde River (RM 172.8)
